Poiseuille Flow and the Viscous Dissipative Mechanism
of the Emergence of Turbulence in a Boundary Layer
S. G. Chefranova and A. G. Chefranovb
a Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences, Pyzhevskii per. 3, Moscow, 119017 Russia
e-mail: schefranov@mail.ru
b Eastern Mediterranean University, Famagusta, North Cyprus
e-mail: Alexander.chefranov@emu.edu.tr
Received December 13, 2013
Abstract—It has been shown that the conclusion of the linear instability of the Hagen–Poiseuille flow at finite
Reynolds numbers requires the refusal of the use of the traditional “normal” form of the representation of dis-
turbances, which implies the possibility of separation of variables describing disturbances as functions of the
radial and longitudinal (along the axis of a tube) coordinates. In the absence of such separation of variables in
the developed linear theory, it has been proposed to use a modification of the Bubnov–Galerkin theory that
makes it possible to take into account the difference between the periods of the longitudinal variability for dif-
ferent radial modes preliminarily determined by the standard application of the Galerkin–Kantorovich method
to the evolution equation of extremely small axisymmetric disturbances of the tangential component of the
velocity field. It has been shown that the consideration of even two linearly interacting radial modes for the
Hagen–Poiseuille flow can provide linear instability only in the presence of the mentioned conditionally peri-
odic longitudinal variability of disturbances along the axis of the tube, when the threshold Reynolds number
Reth(p) is very sensitive to the ratio p of two longitudinal periods each describing longitudinal variability for its
radial disturbance mode. In this case, the threshold Reynolds number can tend to infinity, Reth(p) 
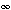, only
at p = pk = k, p = p1/k = 1/k, and p = 
= [k + 1 
]/2, where k= 1, 2, 3, …. The minimum
Reynolds number Reth(p) 
448 (at which p 1.527) for the linear instability of the Hagen–Poiseuille flow
quantitatively corresponds to the condition of the excitation of Tollmien–Schlichting waves in the boundary
layer, where Reth = 420. Similarity of the mechanisms of linear viscous dissipative instability for the Hagen–
Poiseuille flow and Tollmien–Schlichting waves has been discussed. Good quantitative agreement has been
obtained between the phase velocities of the vortex disturbances and the experimental data on the velocities of
the leading and trailing edges of turbulent “puffs” propagating along the axis of the tube.
DOI: 10.1134/S1063776114070127
Pleiades Publishing home page | journal home page | top
If you have any problems with this server, contact webmaster.